前面在位运算及其应用这篇文章里提到了可以使用二进制的位的Index来表示无符号整数,二进制的值0和1可以表示整数是否存在。相比单独的使用诸如int来存储数据而言,使用位来表示数据能够减少存储占用至少32倍(原先一个int类型32位存一个值,现在一个int类型的32位可以表示0-31个整数)。
基于上述思想,可以使用类似Bitmap的结构来存储海量数据,这在一些编程语言,诸如C++中bitset和C#中的BitArray都有内置的实现。Bitmap存储哈希函数生成的特征值,就是今天要介绍的布隆过滤器。在介绍布隆过滤器之前,建议先看前面位运算及应用和哈希函数相关的内容。
问题提出
在介绍布隆过滤器之前,先想象下以下的一个场景:假设要在网上注册一个用户,这个网站现有用户几千万,当创建用户时,输入一个用户名,系统提示“该用户名已存在”,于是你在用户名后面加上生日,系统还是提示“该用户已存在”,系统是如何在几千万用户名中查找你输入的用户名是否存在的呢?有以下一些方法:
- 直接线性查找,这样很慢啊,效率O(n)
- 先对用户名进行排序,然后二分查找,效率O(logn),是要快一点,但还是要经过很多次比较。
- 直接用哈希,把所有用户名加载到内存,然后直接判断是否在其中,O(1)
以上方法,要么很慢,要么对内存占用很高。假设用户有2亿,前面说过,如果直接存储内存就要好多个G。那么有没有一种既快,又内存占用少的判断一个对象是否在集合中的方法呢?这就是布隆过滤器。
布隆过滤器
布隆过滤器(Bloom Filter)是 1970 年由布隆提出的。它实际上是一个很长的二进制向量和一系列随机映射函数,主要用于判断一个元素是否在一个集合中。与直接存储数据不同,布隆过滤器是通过一系列随机映射函数,将待存储的数据通过映射函数提取特征,然后将这些特征存储到二进制向量对应的二进制位上(类似于前文的Bitmap存储),当查找某个值时,通过随机映射函数,提取特征,然后检查这些特征所在的二进制位上是否都为1,如果都为1,表示该可能存在在集合中;但只要有一个为0,则一定不在集合中。布隆过滤器有以下特征:
- 与标准的哈希表不同,布隆过滤器可以通过一个固定的二进制向量,存储大量的数据的特征。
- 添加数据和查询数据的时间复杂度为O(n),n为随机映射函数的个数。添加数据不会失败,但是随着数据的增多,二进制向量的数据位被设为1的增多,误判率会上升,当所有的二进制位都被设置为1时,所有的查询都会返回存在。
- 返回的结果如果是存在,则可能存在误判(false negative)。比如某个用户名布隆过滤告诉我们集合里已经存在这个用户名,但实际上集合里可能根本不存在该用户名。误判存在的根本原因是哈希值的冲突。
- 不能够删除对象。因为如果我们删除某个对象通过多个哈希函数产生的结果对应的位。这些位有可能也存储了其它对象通过哈希值产生的数据,删除就会造成其它数据的特征值遭到破坏。
原理
原理在介绍部分其实已经很清楚了,这里再用图来说明一下,假设我们用16个位来存储哈希值,这些哈希值由3个哈希函数h1、h2、h3产生。
现在插入一个用户名"zhangsan",经过哈希函数计算,得到的结果分别为0、3、6:
h1("zhangsan") % 16 = 0;
h2("zhangsan") % 16 = 3;
h3("zhangsan") % 16 = 6;于是,将16个二进制位里面的第0、3、6位设置为1,其它位保持不动,如下图:
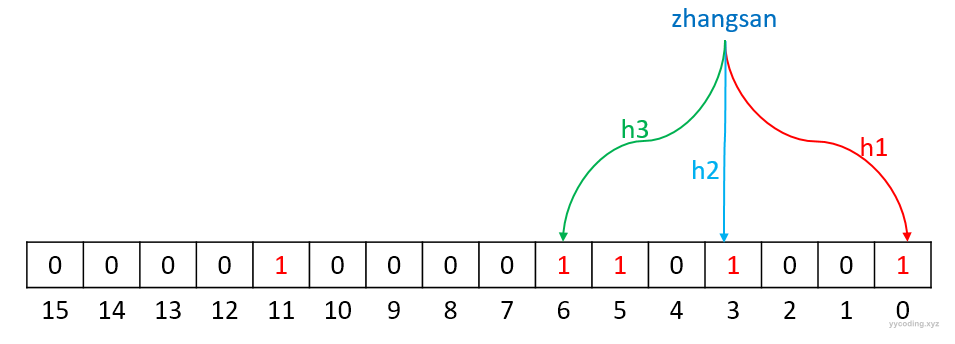
现在,当检查“zhangsan”是否存在时,也用这三个哈希函数h1,h2,h3先计算哈希值,得到结果为0,3,6,然后检查二进制数组中对应的第0位,第3位,第6位。如果都为1,则表示“zhangsan”可能存在于集合中,如果只要有一个位数为0,那么“zhangsan”一定不在集合中。
紧接着插入“lisi”,同样先用三个哈希函数分别计算得到哈希值,假设为5,6,11。
h1("lisi") % 16 = 5;
h2("lisi") % 16 = 6;
h3("lisi") % 16 = 11;于是,将16个二进制位里面的第5、6、11位设置为1,其它位保持不动(其中检查发现第6位已经为1,不需要重新设置),如下图:
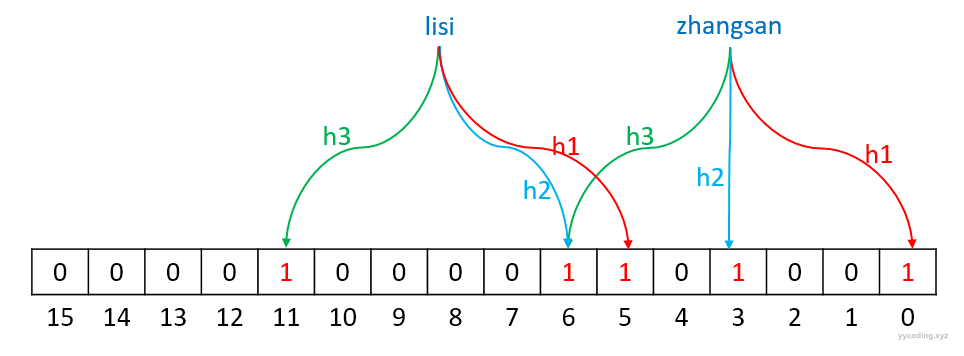
现在检查“lisi”是否在集合中,还是同样步骤,先通过哈希函数分别计算出哈希值5,6,11,然后查找16位二进制中对应的为是否存在0,如果有一个为0,则其它位不用检查,肯定不存在。如果都为1,则表示“lisi”有可能存在于集合中。
误判
现在,假设另外一个用户,想注册了一个名为“wangwu”的用户名,系统首先根据哈希函数h1,h2,h3计算出“wangwu”的哈希值,假设得到的结果是0,5,11。
h1("wangwu") % 16 = 0;
h2("wangwu") % 16 = 5;
h3("wangwu") % 16 = 11;于是,系统检查16位数据的第0,5,11位,发现这三个位数据均为1,表示“wangwu”存在于系统中,这就是误判。因为0,5,11这三个位的1是用户“zhangsan”和“lisi”所产生的特征值,而只是恰好“wangwu”所产生的的特征值跟他们的特征值重合了,系统中根本不存在“wangwu”。
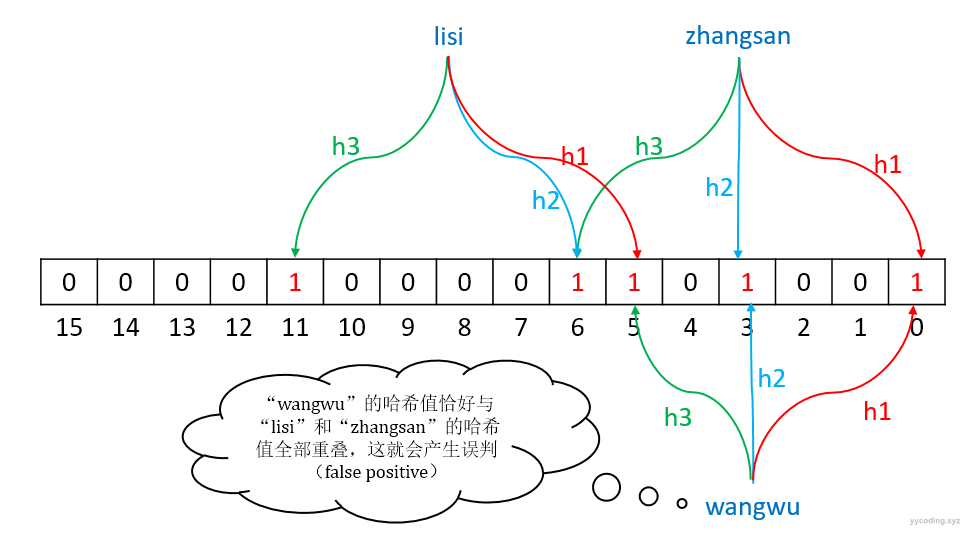
布隆过滤器的误判是指,由于多个输入经过哈希函数之后在相同的bit位设置为1了,这样就无法判断究竟是哪个输入产生的,因此误判的根源在于相同的bit位被多次映射且置为1。
这种情况也造成了布隆过滤器的删除问题,因为布隆过滤器的每一个bit位并不是独占的,很有可能多个元素共享了某一位,如果我们直接删除这一位的话,会影响到其他元素。
根据系统的不同,这种误判可能会产生严重后果,或者说相对来说误判关系不大。
可以通过改变布隆过滤器的二进制位的长度以及控制哈希函数的个数来控制误判率。一般来说,更大的二进制位数和更多的哈希函数能够减少误判率。但这会增加存储空间和计算哈希函数的时间开销。
哈希函数
可以看到,在布隆过滤器中,哈希函数扮演了非常重要的作用,哈希函数必须独立并且尽量符合通过哈希函数计算的结果均匀分布,哈希函数运算越快越好。快速简单的非加密算法murmur、FNV系列哈希函数以及Jenkins哈希,它们一般彼此之间不相关。
产生哈希值是布隆过滤器的主要操作,加密的哈希函数能够提供稳定且唯一的哈希值保证,但运算起来可能过于耗时,随着哈希函数个数的增加,布隆过滤器运行速度可能会减慢。而非加密哈希算法虽然不能保证哈希值的唯一性但运行的足够快,所以具体如何选择哈希函数,需要根据系统的需求进行调研和比较。
一个简单的实现
根据以上原理,结合前面章节的Bitmap思想,很容易实现一个简单的布隆过滤器。
#include <iostream>
#include "bitset"
#include "string"
#include "math.h"
#include "vector"
const int length = 100;
int h1(const std::string &s, const int arrSize)
{
long long int hash = 0;
for (auto i : s)
{
hash = (hash + (int)i);
hash = hash % arrSize;
}
return hash;
}
int h2(const std::string &s, const int arrSize)
{
long long int hash = 1;
for (size_t i = 0; i < s.size(); i++)
{
hash = (hash + std::pow(19, i) * s[i]);
hash = hash % arrSize;
}
return hash % arrSize;
}
int h3(const std::string &s, const int arrSize)
{
long long int hash = 7;
for (size_t i = 0; i < s.size(); i++)
{
hash = (hash * 31 + s[i]) % arrSize;
}
return hash % arrSize;
}
int h4(const std::string &s, const int arrSize)
{
long long int hash = 3;
int p = 7;
for (size_t i = 0; i < s.size(); i++)
{
hash += (hash * 7 + s[0] * std::pow(p, i));
hash = hash % arrSize;
}
return hash;
}
typedef int (*hashfunc)(const std::string &, const int);
bool lookup(const std::vector<hashfunc> &funcs, const std::bitset<length> &bitSet, const std::string s, const int arraySize)
{
for (auto b = funcs.begin(); b != funcs.end(); b++)
{
int hr = (*b)(s, arraySize);
//只要一个为false,立即返回
if (!bitSet[hr])
{
return false;
}
}
return true;
}
void insert(const std::vector<hashfunc> &funcs, std::bitset<length> &bitSet, const std::string s, const int arraySize)
{
if (lookup(funcs, bitSet, s, arraySize))
{
std::cout << s << " is Probably already present" << std::endl;
}
else
{
for (auto b = funcs.begin(); b != funcs.end(); b++)
{
int hr = (*b)(s, arraySize);
bitSet.set(hr, true);
}
std::cout << s << " inserted" << std::endl;
}
}
int main()
{
std::bitset<length> bitSets;
std::vector<std::string> badWords{"abound", "abounds", "abundance",
"abundant", "accessible", "bloom",
"blossom", "bolster", "bonny",
"bonus", "bonuses", "coherent",
"cohesive", "colorful", "comely",
"comfort", "generosity",
"generous", "generously", "genial",
"bluff", "cheater", "hate",
"war", "humanity", "racism",
"hurt", "nuke", "gloomy",
"facebook", "geeksforgeeks"};
std::vector<hashfunc> funcs{h1, h2, h3, h4};
for (auto i = badWords.begin(); i != badWords.end(); i++)
{
insert(funcs, bitSets, *i, length);
}
return 0;
}这里布隆过滤器二进制位数设置为了100,使用了4个哈希函数,对33个脏字,插入布隆过滤器,然后运行结果如下:
abound inserted
abounds inserted
abundance inserted
abundant inserted
accessible inserted
bloom inserted
blossom inserted
bolster inserted
bonny inserted
bonus inserted
bonuses inserted
coherent inserted
cohesive inserted
colorful inserted
comely inserted
comfort inserted
generosity inserted
generous inserted
generously inserted
genial inserted
bluff is Probably already present
cheater inserted
hate inserted
war is Probably already present
humanity inserted
racism inserted
hurt inserted
nuke is Probably already present
gloomy is Probably already present
facebook inserted
geeksforgeeks inserted
twitter inserted可以看到,后面插入的有很多误判。现在将布隆过滤器的二进制位长度length从100改为1000,再次运行,结果如下:
abound inserted
abounds inserted
abundance inserted
abundant inserted
accessible inserted
bloom inserted
blossom inserted
bolster inserted
bonny inserted
bonus inserted
bonuses inserted
coherent inserted
cohesive inserted
colorful inserted
comely inserted
comfort inserted
generosity inserted
generous inserted
generously inserted
genial inserted
bluff inserted
cheater inserted
hate inserted
war inserted
humanity inserted
racism inserted
hurt inserted
nuke inserted
gloomy inserted
facebook inserted
geeksforgeeks inserted
twitter inserted可以看到基本消除了误判。
特性
- 一个元素如果判断结果为存在,则元素不一定存在,因为可能存在误判。
- 但是,一个元素如果判断结果为不存在,那就一定不存在。
- 布隆过滤器可以添加元素,查询元素。但是不能删除元素,删除元素会产生错误并导致误判率增加。
优缺点
布隆过滤器有如下优点:
- 相较于其它数据结构,布隆过滤器在空间和时间方面都有巨大优势,其插入和查询事件都是常数级别O(n),n为哈希函数个数。另外,哈希函数之间没有关系,可以并行实现。
- 布隆过滤器不存储数据本身,它存储的是数据经过哈希函数产生的特征值,对某些对保密要求严格的场景有优势。
- 因为不存储数据本身,所以容易做成中间件。
缺点前面也提到过,总结如下:
- 误判率会随着元素的插入数量增加而增加,但如果元素数量比较少,直接使用哈希表即可。
- 布隆过滤器不能删除元素。因为首先必须保证待删除的元素一定在布隆过滤器里面,单凭这一点,布隆过滤器是无法保证的。
- 在降低布隆过滤器误判率方面,又很不布隆过滤器的变种,可能使得实现更加复杂。
对于解决删除的问题:
- 可以重新载入布隆过滤器了。开发定时任务,每隔几个小时,自动创建一个新的布隆过滤器数组替换老的。这也就意味着,这一方法在高并发的情况下有缺陷。
- 或者,直接记录hash冲突次数。布隆过滤器增加一个等长的数组,存储计数器,主要解决冲突问题,每次删除时对应的计数器减一,如果结果为0,更新主数组的二进制值为0。这样会增加存储空间。
所以如果有删除需求,那么大多数情况只能应用在缓存数据更新较慢的情况下。
应用场景
布隆过滤器扩展了哈希表的应用范围,解决了哈希表的内存占用瓶颈,且有较高的空间时间效率,在系统中应用十分广泛。常见的应用有:
- 注册新用户时,判断用户名是否已经存在。
- 邮件过滤,使用布隆过滤器来做邮件黑名单过滤。不在黑名单里的邮件才显示
- 对爬虫网站进行过滤,已经爬过的不再重复处理
- 解决新闻推荐过的不再推荐。判断用户是否已经阅读过某视频或文章,会有误判,但没有阅读过就一定没有阅读过,可以保证用户不会看到重复的内容
- 一些数据内内置布隆过滤器,用于判断数据是否存在,可以减少数据库的IO请求。
- 用于解决缓存穿透和缓存击穿(缓存穿透就是请求直达数据库,屡次请求数据库不存在的数据。缓存击穿是同时请求缓存中没有但数据库有的数据,但因为是同时大并发请求,所以缓存还没来得及更新请求都取数据库查询,淫妻数据库压力瞬间增大。),缓存的一般流程是先判断要查询的内容是否在缓存中,如果在,直接返回而不查询db,如果不在,才去查询db。如果同时来大量的查询,查询的数据都不在缓存中,这就会导致缓存穿透或击穿,产生雪崩效应。所以可以用布隆过滤器把db数据库里的部分内容比如ID先放进来,只有在布隆过滤器中有的,才去查询缓存或者db。如果不在布隆过滤器中,直接返回。
- Web拦截器,如果相同请求则拦截,防止重复被攻击。用户第一次请求,将请求参数放入布隆过滤器中,当第二次请求时,先判断请求参数是否被布隆过滤器命中。可以提高缓存命中率。Google Chrome浏览器使用了布隆过滤器加速安全浏览服务。
参考
- https://www.yycoding.xyz/post/2022/11/27/bitwise-operation-and-its-applications
- https://blog.csdn.net/qq_41125219/article/details/119982158—全面讲解,建议收藏_李子捌的博客-CSDN博客_bloom filter
- https://developer.aliyun.com/article/773205
- https://www.cnblogs.com/mushroom/p/4556801.html
- https://www.geeksforgeeks.org/bloom-filters-introduction-and-python-implementation/
- https://en.wikipedia.org/wiki/Bloom_filter
