在.NET中的基础类库(Basic Class Liberary，BCL)中有一些基本的数据类型比如Stack、List、Dictionary、LinkList等等，这些类型虽然看上去五花八门，但是其内部的实现所使用的数据结构无外乎是那些经典的结构比如数组、链表、哈希表、树等。了解这些类型背后的结构就能很清楚的知道对应数据类型的插入、查找、删除的时间和空间复杂度。在应用开发中可以根据具体的使用场景，选择合适的、高效的数据结构可以提高应用程序的效率。.NET Runtime已经开源，本文试图通过源码来查看这些基本类型的内部实现方式。

下面根据这些基本数据类型的内部实现所采用的数据结构来进行分类说明.NET中的各种类型的实现。

名称 实现方式 添加 查找 删除 索引访问
ArrayList 固定大小数组 O(n) O(n) O(n) O(n)
List<T> 可自动扩容数组 O(n) O(n) O(n) O(n)
SortedList<T> 排序的支持自动扩容的数组        
LinkedList<T> 双向链表 O(1) O(n) O(n) O(n)
Queue<T> 环形可自动扩容数组 O(1) - O(1)  
PriorityQueue<T，P> 四叉最小堆 O((log n)/2) - O(2 log n)  
Stack<T> 可自动扩容数组 O(1) - O(1)  
HashSet<T> 哈希表 O(1) O(1) O(1)  
Dictionary<K,V> 哈希表 O(1) O(1) O(1)  
SortedSet<T> 红黑树 O(log n) O(log n) O(log n)  
SortedDictionary<K,V> 红黑树 O(log n) O(log n) O(log n)  

 

数组

数组(Array)是最简单的而且应用最广泛的数据结构之一，在多种编程语言中，数组具有以下共同特性：

  • 由相同类型的元素（element）的集合所组成。
  • 分配一块连续的内存来存储。
  • 利用元素的索引（index）可以得到该元素对应的存储地址。

分配连续的内存来存储使得数组中的元素彼此相邻，具有更好的空间局部性和时间局部性，另外通过索引能够以常量时间复杂度获取对应的数据。但数组也有一些缺点

  • 数组的大小是固定的，一旦分配后不能调整，可以通过算法扩张和搜索，但相对耗时
  • 插入和删除元素，需要移动插入点或删除点之后的所有元素

在.NET中数组使用 T[] 的形式来进行声明，ArrayList、List、Stack、Queue都是基于数组实现的。

ArrayList

在C#中，ArrayList是非泛型长度可扩充数组。其内部由Array支持实现，而Array的关键部分大都是unsafe代码，所以相对来说性能较高 (在runtime内部还有一个非托管的C++ Array arraynative.cpp)。

ArrayList对象的内部实现中有一个名为_item的object[]对象以及一个表示长度的_size。数组初始大小为0，当添加第1个元素时，会扩容到_defaultCapacity=4个大小。Add方法如下：

// Adds the given object to the end of this list. The size of the list is
// increased by one. If required, the capacity of the list is doubled
// before adding the new element.
//
public virtual int Add(object? value)
{
    if (_size == _items.Length) EnsureCapacity(_size + 1);
    _items[_size] = value;
    _version++;
    return _size++;
}

它首先检查当前记录的元素个数，如果当前的元素个数已经等于数组长度，则调用EnsureCapacity进行扩容。

// Ensures that the capacity of this list is at least the given minimum
// value. If the current capacity of the list is less than min, the
// capacity is increased to twice the current capacity or to min,
// whichever is larger.
private void EnsureCapacity(int min)
{
    if (_items.Length < min)
    {
        int newCapacity = _items.Length == 0 ? _defaultCapacity : _items.Length * 2;
        // Allow the list to grow to maximum possible capacity (~2G elements) before encountering overflow.
        // Note that this check works even when _items.Length overflowed thanks to the (uint) cast
        if ((uint)newCapacity > Array.MaxLength) newCapacity = Array.MaxLength;
        if (newCapacity < min) newCapacity = min;
        Capacity = newCapacity;
    }
}

可以看到，当数组初始时，第一次插入会将数组大小扩充为4，后面再按照2倍当前大小扩容。真正的扩容实现在Capacity这个属性的Set方法里，方法如下：

// Gets and sets the capacity of this list.  The capacity is the size of
// the internal array used to hold items.  When set, the internal
// array of the list is reallocated to the given capacity.
//
public virtual int Capacity
{
    get => _items.Length;
    set
    {
        if (value < _size)
        {
            throw new ArgumentOutOfRangeException(nameof(value), SR.ArgumentOutOfRange_SmallCapacity);
        }

        // We don't want to update the version number when we change the capacity.
        // Some existing applications have dependency on this.
        if (value != _items.Length)
        {
            if (value > 0)
            {
                object[] newItems = new object[value];
                if (_size > 0)
                {
                    Array.Copy(_items, newItems, _size);
                }
                _items = newItems;
            }
            else
            {
                _items = new object[_defaultCapacity];
            }
        }
    }
}

扩容的方法由Array.Copy实现，先分配一个2倍大的数组，然后将原始数据的内容拷贝到新创建的数组中。Array.Copy是通过使用unsafe代码来实现的，如下：

// Copies length elements from sourceArray, starting at index 0, to
// destinationArray, starting at index 0.
public static unsafe void Copy(Array sourceArray, Array destinationArray, int length)
{
    if (sourceArray is null)
        ThrowHelper.ThrowArgumentNullException(ExceptionArgument.sourceArray);
    if (destinationArray is null)
        ThrowHelper.ThrowArgumentNullException(ExceptionArgument.destinationArray);

    MethodTable* pMT = RuntimeHelpers.GetMethodTable(sourceArray);
    if (MethodTable.AreSameType(pMT, RuntimeHelpers.GetMethodTable(destinationArray)) &&
        !pMT->IsMultiDimensionalArray &&
        (uint)length <= sourceArray.NativeLength &&
        (uint)length <= destinationArray.NativeLength)
    {
        nuint byteCount = (uint)length * (nuint)pMT->ComponentSize;
        ref byte src = ref Unsafe.As<RawArrayData>(sourceArray).Data;
        ref byte dst = ref Unsafe.As<RawArrayData>(destinationArray).Data;

        if (pMT->ContainsGCPointers)
            Buffer.BulkMoveWithWriteBarrier(ref dst, ref src, byteCount);
        else
            Buffer.Memmove(ref dst, ref src, byteCount);

        // GC.KeepAlive(sourceArray) not required. pMT kept alive via sourceArray
        return;
    }

    // Less common
    CopyImpl(sourceArray, sourceArray.GetLowerBound(0), destinationArray, destinationArray.GetLowerBound(0), length, reliable: false);
}

这里面，使用的Buffer.Memmove方法，想必应该十分高效。

删除特定元素，使用了Array.Copy方法：

public virtual void RemoveAt(int index)
{
    if (index < 0 || index >= _size) throw new ArgumentOutOfRangeException(nameof(index), SR.ArgumentOutOfRange_IndexMustBeLess);

    _size--;
    if (index < _size)
    {
        Array.Copy(_items, index + 1, _items, index, _size - index);
    }
    _items[_size] = null;
    _version++;
}

可以看到，如果要删除第index个元素，可以将index+1开始的所有元素向前移动一个，覆盖掉index那个元素，然后将最后一个元素设置为null，可以看到整个数组的长度没有变化。

插入元素也是类似，先将待插入位置index的元素空出来，将包含index及之后的所有元素拷贝到 index+1的为止，拷贝长度为_size-1，然后把新元素放到index位置。

public virtual void Insert(int index, object? value)
{
    // Note that insertions at the end are legal.
    if (index < 0 || index > _size) throw new ArgumentOutOfRangeException(nameof(index), SR.ArgumentOutOfRange_IndexMustBeLessOrEqual);

    if (_size == _items.Length) EnsureCapacity(_size + 1);
    if (index < _size)
    {
        Array.Copy(_items, index, _items, index + 1, _size - index);
    }
    _items[index] = value;
    _size++;
    _version++;
}

注意，这里当添加元素是会自动扩容，但删除元素时，不会自动进行缩容，如果确认不再需要往数组插入元素，需要缩容的化，可以调用TrimToSize方法：

// Sets the capacity of this list to the size of the list. This method can
// be used to minimize a list's memory overhead once it is known that no
// new elements will be added to the list. To completely clear a list and
// release all memory referenced by the list, execute the following
// statements:
//
// list.Clear();
// list.TrimToSize();
//
public virtual void TrimToSize()
{
    Capacity = _size;
}

List

List跟ArrayList的实现基本一样，只不过List是泛型版本，强烈建议不要使用ArrayList而改为使用List，相比非泛型版本的ArrayList，泛型的List具有以下优点：

  • 类型安全，初始化List的时候必须指定存储类型，这样在往里添加元素时能得到编译时检查，而以往的ArrayList只能往里面添加Object类型的对象。
  • 更好性能，避免了存储值类型时产生的装箱和拆箱操作，存储引用类型时，也能够避免类型转换。

List不支持缩容，如果需要，可以调用TrimExcess方法，如下：

// Sets the capacity of this list to the size of the list. This method can
// be used to minimize a list's memory overhead once it is known that no
// new elements will be added to the list. To completely clear a list and
// release all memory referenced by the list, execute the following
// statements:
//
// list.Clear();
// list.TrimExcess();
//
public void TrimExcess()
{
    int threshold = (int)(((double)_items.Length) * 0.9);
    if (_size < threshold)
    {
        Capacity = _size;
    }
}

List和ArrayList都是基于数组实现的，所以添加、删除、查找的时间复杂度均为O(n)，并且支持通过索引访问元素，此时时间复杂度为O(1)。

Stack

Stack是后进先出(Last in First Out) 的数据结构。在内部仍然是基于一个数组 T[] 和一个标识数组大小的 _size 字段来实现的。它提供了Push和Pop的操作。Push的方法如下：

// Pushes an item to the top of the stack.
public void Push(T item)
{
    int size = _size;
    T[] array = _array;

    if ((uint)size < (uint)array.Length)
    {
        array[size] = item;
        _version++;
        _size = size + 1;
    }
    else
    {
        PushWithResize(item);
    }
}

// Non-inline from Stack.Push to improve its code quality as uncommon path
[MethodImpl(MethodImplOptions.NoInlining)]
private void PushWithResize(T item)
{
    Debug.Assert(_size == _array.Length);
    Grow(_size + 1);
    _array[_size] = item;
    _version++;
    _size++;
}

可以看到，往栈顶添加元素时，如果当前数组内元素个数小于数组长度，直接把元素添加到数组的末尾，否则需要将数组进行扩容，然后把原先数组内容拷贝到新的数组中，然后再把元素添加到新的数组的末尾。扩容方法如下：

private void Grow(int capacity)
{
    Debug.Assert(_array.Length < capacity);

    int newcapacity = _array.Length == 0 ? DefaultCapacity : 2 * _array.Length;

    // Allow the list to grow to maximum possible capacity (~2G elements) before encountering overflow.
    // Note that this check works even when _items.Length overflowed thanks to the (uint) cast.
    if ((uint)newcapacity > Array.MaxLength) newcapacity = Array.MaxLength;

    // If computed capacity is still less than specified, set to the original argument.
    // Capacities exceeding Array.MaxLength will be surfaced as OutOfMemoryException by Array.Resize.
    if (newcapacity < capacity) newcapacity = capacity;

    Array.Resize(ref _array, newcapacity);
}

这里扩容使用的是Array.Resize方法，和之前List的扩容方法有些不同，Array.Resize方法如下:

public static void Resize<T>([NotNull] ref T[]? array, int newSize)
{
    if (newSize < 0)
        ThrowHelper.ThrowArgumentOutOfRangeException(ExceptionArgument.newSize, ExceptionResource.ArgumentOutOfRange_NeedNonNegNum);

    T[]? larray = array; // local copy
    if (larray == null)
    {
        array = new T[newSize];
        return;
    }

    if (larray.Length != newSize)
    {
        // Due to array variance, it's possible that the incoming array is
        // actually of type U[], where U:T; or that an int[] <-> uint[] or
        // similar cast has occurred. In any case, since it's always legal
        // to reinterpret U as T in this scenario (but not necessarily the
        // other way around), we can use Buffer.Memmove here.

        T[] newArray = new T[newSize];
        Buffer.Memmove(
            ref MemoryMarshal.GetArrayDataReference(newArray),
            ref MemoryMarshal.GetArrayDataReference(larray),
            (uint)Math.Min(newSize, larray.Length));
        array = newArray;
    }

    Debug.Assert(array != null);
}

从栈顶Pop弹出一个元素的操作也很简单，只需要将集合元素内的个数减1即可，下次Push的时候，直接把弹出的那个位置的元素直接覆盖即可。

// Pops an item from the top of the stack.  If the stack is empty, Pop
// throws an InvalidOperationException.
public T Pop()
{
    int size = _size - 1;
    T[] array = _array;

    // if (_size == 0) is equivalent to if (size == -1), and this case
    // is covered with (uint)size, thus allowing bounds check elimination
    // https://github.com/dotnet/coreclr/pull/9773
    if ((uint)size >= (uint)array.Length)
    {
        ThrowForEmptyStack();
    }

    _version++;
    _size = size;
    T item = array[size];
    if (RuntimeHelpers.IsReferenceOrContainsReferences<T>())
    {
        array[size] = default!;     // Free memory quicker.
    }
    return item;
}

代码非常简单，浅显、易懂、且高效。

Stack仅支持LIFO的操作，因为仅在数组的末尾进行操作，所以添加和删除的效率都是O(1)。

Queue

Queue是一种FIFO（first in first out）先进先出的数据结构，在.NET中，其内部实现是基于环形数组 (circular buffer)实现的，它由一个数组 T[] ，两个分别表示头部_head和尾部_tail位置，以及一个标识数组大小的 _size 字段组成。

private T[] _array;
private int _head;       // The index from which to dequeue if the queue isn't empty.
private int _tail;       // The index at which to enqueue if the queue isn't full.
private int _size;       // Number of elements.
private int _version;

Queue提供了Enqueue和Dequeue方法，Enqueue方法如下：

// Adds item to the tail of the queue.
public void Enqueue(T item)
{
    if (_size == _array.Length)
    {
        Grow(_size + 1);
    }

    _array[_tail] = item;
    MoveNext(ref _tail);
    _size++;
    _version++;
}

Enqueue方法往数组的末尾插入一个元素，然后使用MoveNext将_tail标记加1，以备下一次插入。

// Increments the index wrapping it if necessary.
private void MoveNext(ref int index)
{
    // It is tempting to use the remainder operator here but it is actually much slower
    // than a simple comparison and a rarely taken branch.
    // JIT produces better code than with ternary operator ?:
    int tmp = index + 1;
    if (tmp == _array.Length)
    {
        tmp = 0;
    }
    index = tmp;
}

这里有一个地方需要注意的是，如果下一个位置到了数组的末尾，则将_tail设置为0，移动到数组的前面元素。

另外，在往数组里添加元素时，如果当前数组元素的大小已经等于数组长度，则使用Grow方法进行扩容，扩容方法与之前的大同小异，但这里要判断_tail和_head指示位置的先后顺序。

private void Grow(int capacity)
{
    Debug.Assert(_array.Length < capacity);

    const int GrowFactor = 2;
    const int MinimumGrow = 4;

    int newcapacity = GrowFactor * _array.Length;

    // Allow the list to grow to maximum possible capacity (~2G elements) before encountering overflow.
    // Note that this check works even when _items.Length overflowed thanks to the (uint) cast
    if ((uint)newcapacity > Array.MaxLength) newcapacity = Array.MaxLength;

    // Ensure minimum growth is respected.
    newcapacity = Math.Max(newcapacity, _array.Length + MinimumGrow);

    // If the computed capacity is still less than specified, set to the original argument.
    // Capacities exceeding Array.MaxLength will be surfaced as OutOfMemoryException by Array.Resize.
    if (newcapacity < capacity) newcapacity = capacity;

    SetCapacity(newcapacity);
}

// PRIVATE Grows or shrinks the buffer to hold capacity objects. Capacity
// must be >= _size.
private void SetCapacity(int capacity)
{
    T[] newarray = new T[capacity];
    if (_size > 0)
    {
        if (_head < _tail)
        {
            Array.Copy(_array, _head, newarray, 0, _size);
        }
        else
        {
            Array.Copy(_array, _head, newarray, 0, _array.Length - _head);
            Array.Copy(_array, 0, newarray, _array.Length - _head, _tail);
        }
    }

    _array = newarray;
    _head = 0;
    _tail = (_size == capacity) ? 0 : _size;
    _version++;
}

Queue的插入操作在数组容量足够的条件下复杂度为O(1)，如果容量不足需要扩容，则复杂度变为O(n)，删除操作复杂度为O(1)。

链表

链表（Linked list）是一种常见的基础数据结构，是一种线性表，但是并不会按线性的顺序存储数据，而是在每一个节点里存下一个节点的指针(Pointer)。由于不必须按顺序存储，链表在插入的时候可以达到O(1)的复杂度，比数组要快得多，但是访问特定编号的节点则需要O(n)的时间，而数组则只需O(1)。

链表克服了数组需要预先知道大小的缺点，也克服了可变数组需要创建新的数组并且拷贝的开销。链表结构可以充分利用计算机内存空间，实现灵活的内存动态管理。但是链表失去了数组随机读取的优点，同时链表由于增加了节点的指针域，空间开销比较大，最后相比数组，数据在内存中不是连续存储，所以空间局部性较差，不能很好的利用CPU缓存。

在.NET中，LinkedList<T>使用链表实现。

LinkedList

LinkedList内部是一个双向循环链表 (doubly-Linked circular list)，每个节点包含前一个节点和后一个节点的指针。

// Note following class is not serializable since we customized the serialization of LinkedList.
public sealed class LinkedListNode<T>
{
    internal LinkedList<T>? list;
    internal LinkedListNode<T>? next;
    internal LinkedListNode<T>? prev;
    internal T item;

    public LinkedListNode(T value)
    {
        item = value;
    }

    internal LinkedListNode(LinkedList<T> list, T value)
    {
        this.list = list;
        item = value;
    }

    public LinkedList<T>? List
    {
        get { return list; }
    }

    public LinkedListNode<T>? Next
    {
        get { return next == null || next == list!.head ? null : next; }
    }

    public LinkedListNode<T>? Previous
    {
        get { return prev == null || this == list!.head ? null : prev; }
    }

    public T Value
    {
        get { return item; }
        set { item = value; }
    }

    /// <summary>Gets a reference to the value held by the node.</summary>
    public ref T ValueRef => ref item;

    internal void Invalidate()
    {
        list = null;
        next = null;
        prev = null;
    }
}

LinkedList<>中包含一个head的头结点和表示元素个数的count

// This LinkedList is a doubly-Linked circular list.
internal LinkedListNode<T>? head;
internal int count;
internal int version;

当往链表某个节点插入数据时，有AddBefore和AddAfter两个方法：

public LinkedListNode<T> AddAfter(LinkedListNode<T> node, T value)
{
    ValidateNode(node);
    LinkedListNode<T> result = new LinkedListNode<T>(node.list!, value);
    InternalInsertNodeBefore(node.next!, result);
    return result;
}
 
public LinkedListNode<T> AddBefore(LinkedListNode<T> node, T value)
{
    ValidateNode(node);
    LinkedListNode<T> result = new LinkedListNode<T>(node.list!, value);
    InternalInsertNodeBefore(node, result);
    if (node == head)
    {
        head = result;
    }
    return result;
}

内部都是调用的InternalInsertNodeBefore方法，如果是在指定节点AddAfter，则在指定的节点的下一个节点node.next 调用InternalInsertNodeBefore。InternalInsertNodeBefore如下，相当简洁明了：

private void InternalInsertNodeBefore(LinkedListNode<T> node, LinkedListNode<T> newNode)
{
    newNode.next = node;
    newNode.prev = node.prev;
    node.prev!.next = newNode;
    node.prev = newNode;
    version++;
    count++;
}

除此之外，LinkedList还是提供了AddFirst和AddLast方法，往链表头和链表尾添加元素。

public LinkedListNode<T> AddFirst(T value)
{
    LinkedListNode<T> result = new LinkedListNode<T>(this, value);
    if (head == null)
    {
        InternalInsertNodeToEmptyList(result);
    }
    else
    {
        InternalInsertNodeBefore(head, result);
        head = result;
    }
    return result;
}

public LinkedListNode<T> AddLast(T value)
{
    LinkedListNode<T> result = new LinkedListNode<T>(this, value);
    if (head == null)
    {
        InternalInsertNodeToEmptyList(result);
    }
    else
    {
        InternalInsertNodeBefore(head, result);
    }
    return result;
}

这里面还有一个情况，就是当列表为空时，插入第一个元素，调用InternalInsertNodeToEmptyList方法：

private void InternalInsertNodeToEmptyList(LinkedListNode<T> newNode)
{
    Debug.Assert(head == null && count == 0, "LinkedList must be empty when this method is called!");
    newNode.next = newNode;
    newNode.prev = newNode;
    head = newNode;
    version++;
    count++;
}

当只有一个元素时，节点的前后指针均指向自己即头元素。

与单向链表相比，双向链表的一个优点是，找到链表的尾元素的时间复杂度为O(1)，如果是单链表则需要从头开始遍历到尾。

public void RemoveFirst()
{
    if (head == null) { throw new InvalidOperationException(SR.LinkedListEmpty); }
    InternalRemoveNode(head);
}

public void RemoveLast()
{
    if (head == null) { throw new InvalidOperationException(SR.LinkedListEmpty); }
    InternalRemoveNode(head.prev!);
}

可以看到，RemoveLast的时候，只需要取得头元素的前一个节点即可指向尾元素。

但双向链表跟单向链表相比，每个节点都多存储了一个指针，所以所占内存空间要多一些。但双向链表跟单向链表相比有以下诸多优点：

  • 删除指定指针指向的节点速度更快。在单向链表中，删除指定节点需要找到前置节点，而单向链表并不保存前置节点，所以需要从链表头部开始遍历。而双向链表待删除节点本身自带指向前置节点的节点，所以速度更快。
  • 在指定节点前面插入一个节点速度更快。因为双向链表保存有某个节点的前置节点，所以速度更快，而单向链表则需要从头开始遍历。
  • 如果链表是有序的，则双向链表可以根据当前节点的值和待比较的值，向前向后移动进行比较，进而速度更快。

LinkedList的插入算法的时间复杂度为O(1)，删除的复杂度为O(n)，因为需要从头节点遍历找到需要删除的节点，然后再删除，查找的时间复杂度为O(n)。

树

在计算机科学中，树（tree）是一种抽象数据类型（ADT）或是实现这种抽象数据类型的数据结构，用来模拟具有树状结构性质的数据集合。它是由n（n>0）个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。它具有以下的特点：
  • 每个节点都只有有限个子节点或无子节点；
  • 没有父节点的节点称为根节点；
  • 每一个非根节点有且只有一个父节点；
  • 除了根节点外，每个子节点可以分为多个不相交的子树；
  • 树里面没有环路(cycle)

树有很多种类，根据字节点之间与父节点之间的大小关系以及是否有序，可以分为二叉查找树，二叉平衡树，红黑树，B树以及二叉堆，四叉堆等。

堆

这里的堆(heap)与计算机里面和“堆”和“栈”的概念完全不同。堆是一种典型的用树来表示的数据结构。可以分为最大堆(Max-heap)和最小堆(Min-heap)，它们具有以下特征：

  • 最大堆：对于树上的每一个节点，节点的值大于等于它的子节点的值。
  • 最小堆：对于书上的每一个节点，节点的值小于等于它的子节点的值。

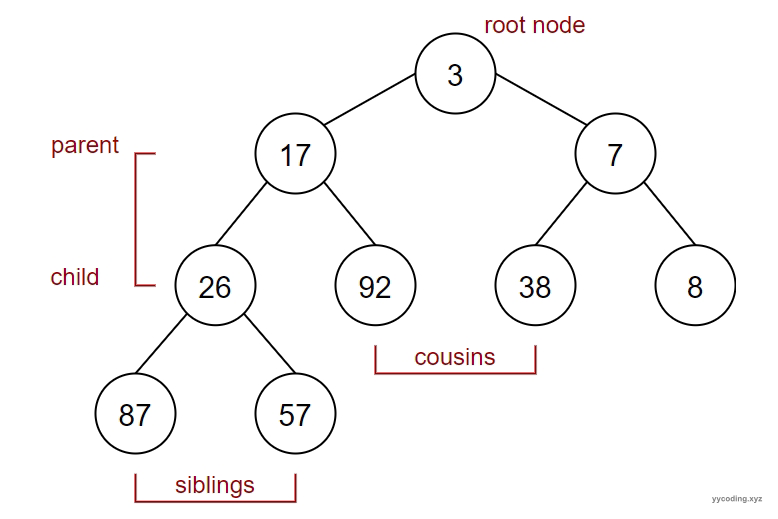
二叉堆

上图中最小堆中可以看到，对于每一个节点，它的父节点都小于等于其子节点。这就是堆的属性。可以注意到，堆对于子节点之间除了他们都比父节点大之外，以及兄弟节点之间的大小关系并没有规定。这和我们通常属性的二叉搜索树中子节点之间有者明确的大小关系有着显著的不同。

通常使用数组来作为堆的底层实现。数组中的每一个元素表示堆的每个节点，元素再数组中的位置定义了节点之间的关系。比如如下：

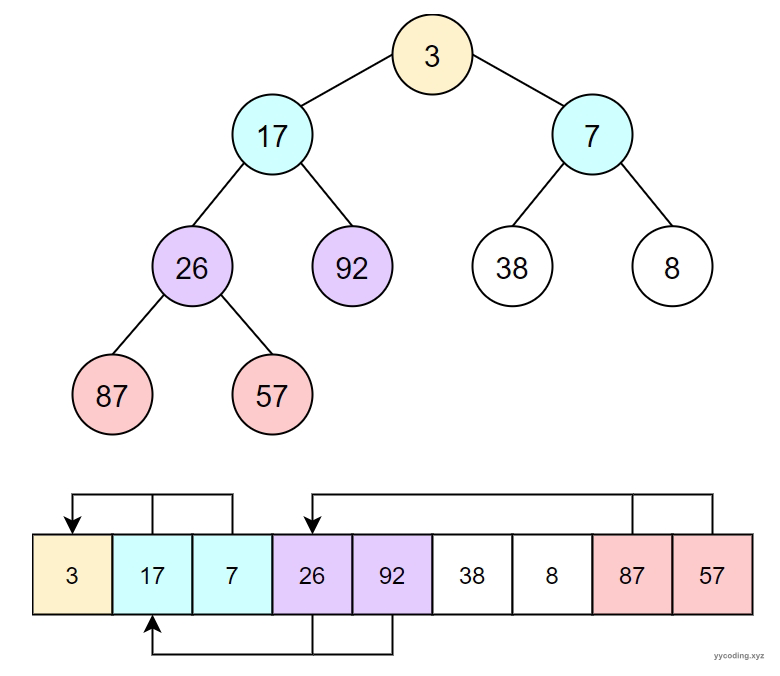
二叉堆的数组表示

如上图是一个二叉堆，每个节点下面最多有两个子节点：

  • 数组0处是根节点，因此它就是整个最小堆中的最小元素。
  • 第1，2处是根节点的子节点。
  • 第3，4处是1的子节点，5，6是2的子节点，依此类推。

可见，假设每个节点最多有k个子节点（k通常是2的指数，比如2，4，8），则：

  • 数组中位于i处的节点的父节点为：（i-1）/ k。
  • 数组中位于i处的节点的第一个子节点为：i*k+1；

关于堆的更多操作，比如插入和删除，可以参看浅谈算法和数据结构: 五 优先级队列与堆排序。

二叉堆和d叉堆(d>2)在允许效率上有些不同。当移除根节点时，二叉堆可能更快，但d叉堆在其它很多操作方面可能表现更好。总的来说，d叉堆相比二叉堆有者更好的运行时效率，这主要归功于缓存，所以在实际应用更倾向多叉堆：

  • d-叉堆增加了堆中每个节点的分叉，使得整个堆的高度变低了（参看上图二叉堆和四叉堆），对于一个节点数量为n的d叉堆，高度为logdn+O(1).
  • 当维护相同数量的元素时，d叉堆比二叉堆上推节点(shit up)操作的更快。假如最下层的某个节点的值被修改为最小，同样上推到堆顶的操作，d叉堆需要的比较次数只有二叉堆的logd2倍。这意味着插入新的元素时，d叉堆比二叉堆更快。
  • d-叉堆堆内存缓存更为友好。多叉堆高度更低，元素在内存存储集中在数组的前部，表现更为“连续”。而二叉堆堆数组的访问范围更大，相对更“随机”。

但d叉堆也有缺点，主要在于下推(sift down)操作。下推操作涉及到节点与所有子节点的数值比较。对于一个n个元素的d叉堆，删除最小值操作的时间复杂度为O(dlogdn)。但wiki上说:

“在实践中，四叉堆可能比二叉堆表现得更好，即使是在删除最小元素 delete-min 的操作上。”
"4-heaps may perform better than binary heaps in practice, even for delete-min operations."

原因在于：算法的实际运行，除了要考虑理论的时间复杂度，还要考虑诸多实际硬件环境的影响：

  • 查找父节点和子节点的成本， 在 d 叉堆中，你可以通过将索引除以 d 来找到你的父节点。对于是 2 的完全幂的 d，这可以通过一个简单、廉价的位移来实现（因为 
     = n >> k）。对于奇数或不是 2 的幂的数字，这需要一个除法，这（在某些架构中）比位移更昂贵。
  • 局部性，如今的计算机具有大量的内存缓存层，访问缓存中的内存的成本可能比访问不在缓存中的内存快数百或数千倍。随着在 d 叉堆中增加 d 的值，树的层数变得更少，访问的元素更加靠近，从而提供了更好的局部性

堆的最常用使用场景就是优先级队列。

PriorityQueue

从.NET 6.0开始，提供了 PriorityQueue<TElement,TPriority> 泛型结构。在内部它使用一个四叉堆来实现（array-backed quaternary min-heap，d-ary min-heap with arity 4）。

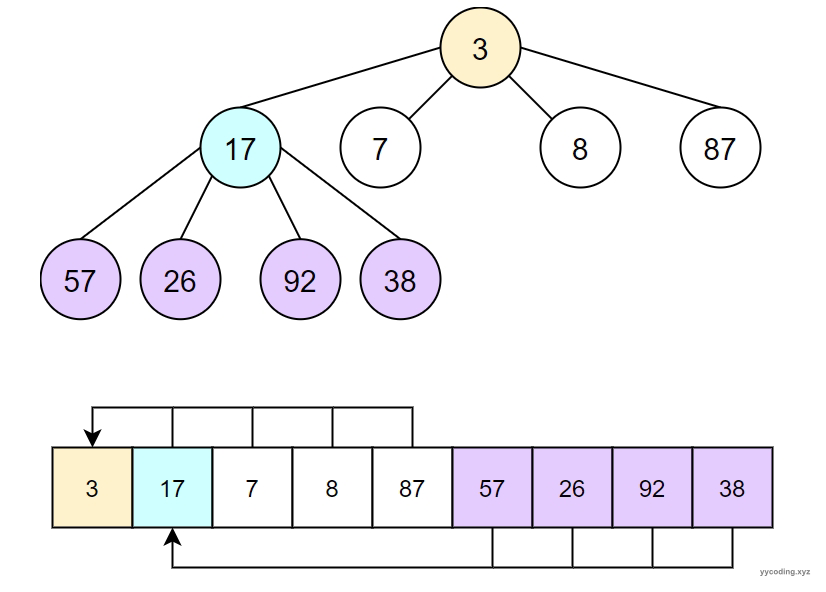
四叉堆

关于.NET中的优先级队列，可以查看 https://andrewlock.net/an-introduction-to-the-heap-data-structure-and-dotnets-priority-queue/ 和 https://andrewlock.net/behind-the-implementation-of-dotnets-priorityqueue/ 这两篇文章。

如果只要求获取最大值或最小值，那么堆就能满足要求，它只对节点和子节点的数组大小进行了约束，而兄弟节点间的大小不则不做任何限制。但如果要进行排序或者更快速的查找，那么除了堆固有的那些特性之外，还需要对兄弟节点之间的大小进行限定，这就是查找树。

查找树

常见的查找树有二叉查找树(Binary Search Tree，BST)，平衡查找树以及红黑树。

二叉查找树满足以下特点：

  1. 若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值。
  2. 若任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值。
  3. 任意节点的左、右子树也分别为二叉查找树。
  4. 没有键值相等的节点（no duplicate nodes）。

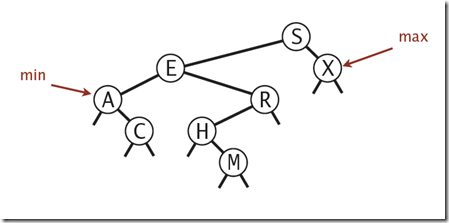
一个典型的二叉查找树

二叉查找树的运行时间和树的形状有关，树的形状又和插入元素的顺序有关。在最好的情况下，节点完全平衡，从根节点到最底层叶子节点只有lgN个节点。在最差的情况下，根节点到最底层叶子节点会有N各节点。在一般情况下，树的形状和最好的情况接近。

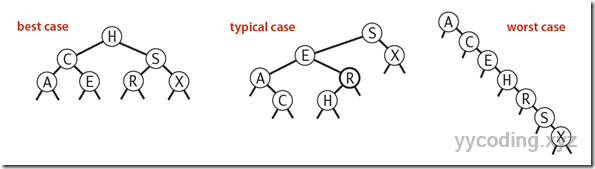
二叉查找树的各种情景

上面的二叉查找树(Binary Search Tree)，在大多数情况下的查找和插入在效率上来说是没有问题的，但是在最差的情况下效率比较低。要保证在最差的情况下也能达到lgN的效率，就要求树在插入完成之后始终保持平衡状态，这就是平衡查找树(Balanced Search Tree)。在一棵具有N 个节点的树中，希望该树的高度能够维持在lgN左右，这样就能保证只需要lgN次比较操作就可以查找到想要的值。这就是平衡查找树它分为二三树查找树及红黑树。

和二叉树不一样，2-3树允许每个节点保存一个或者两个值。对于普通的2节点(2-node)，他保存1个key和左右两个子节点。对于3节点(3-node)，保存两个Key，2-3查找树的定义如下：

  1. 要么为空，要么：
  2. 对于2节点，该节点保存一个key及对应value，以及两个指向左右节点的节点，左节点也是一个2-3节点，所有的值都比key小，右节点也是一个2-3节点，所有的值比key大。
  3. 对于3节点，该节点保存两个key及对应value，以及三个指向左中右的节点。左节点也是一个2-3节点，所有的值均比两个key中的最小的key还要小；中间节点也是一个2-3节点，中间节点的key值在两个根节点key值之间；右节点也是一个2-3节点，节点的所有key值比两个key中的最大的key还要大。

如果中序遍历2-3查找树，就可以得到排好序的序列。在一个完全平衡的2-3查找树中，根节点到每一个为空节点的距离都相同。

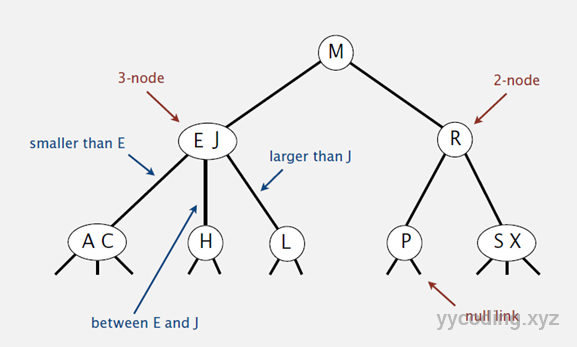
这种2-3查找树实现起来很复杂，因为：

  1. 需要处理不同的节点类型，非常繁琐
  2. 需要多次比较操作来将节点下移
  3. 需要上移来拆分4-node节点
  4. 拆分4-node节点的情况有很多种

因此，添加额外的信息来简化代码的实现变得重要，这就是红黑树。

红黑树的主要是想对2-3查找树进行编码，尤其是对2-3查找树中的3-nodes节点添加额外的信息。红黑树中将节点之间的链接分为两种不同类型，红色链接，他用来链接两个2-nodes节点来表示一个3-nodes节点。黑色链接用来链接普通的2-3节点。特别的，使用红色链接的两个2-nodes来表示一个3-nodes节点，并且向左倾斜，即一个2-node是另一个2-node的左子节点。这种做法的好处是查找的时候不用做任何修改，和普通的二叉查找树相同。

红黑树是一种具有红色和黑色链接的平衡查找树，同时满足：

  • 红色节点向左倾斜
  • 一个节点不可能有两个红色链接
  • 整个书完全黑色平衡，即从根节点到所以叶子结点的路径上，黑色链接的个数都相同。

下图可以看到红黑树其实是2-3树的另外一种表现形式：如果我们将红色的连线水平绘制，那么他链接的两个2-node节点就是2-3树中的一个3-node节点了。

2-3查找树实现起来比较困难，红黑树是2-3树的一种简单高效的实现，他巧妙地使用颜色标记来替代2-3树中比较难处理的3-node节点问题。红黑树是一种比较高效的平衡查找树，应用非常广泛，很多编程语言的内部实现都或多或少的采用了红黑树。

哈希表

哈希表的详情可以查看  浅谈算法和数据结构: 十一 哈希表 ，这篇文章，其中C#中的Dictionary的内部实现，可以查看.NET Core中Dictionary的实现，除此之外，还有一些混合的Dictionary数据结构，可以查看.NET中几种名字包含Dictionary的数据结构

 

参考